
当你看到蓝天白云,日落黄昏,有没有想过这些现象产生的原因是什么?这些物理现象用一句话解释:太阳光与大气层中的参与介质发生了大气散射现象,从而形成了天空颜色。
参与介质
什么是参与介质?光的能量是由光子组成,而空气中与光子进行交互的细小的粒子就被称为参与介质。比如空气中的水分子,以及工厂排放的气溶胶粒子。
光散射
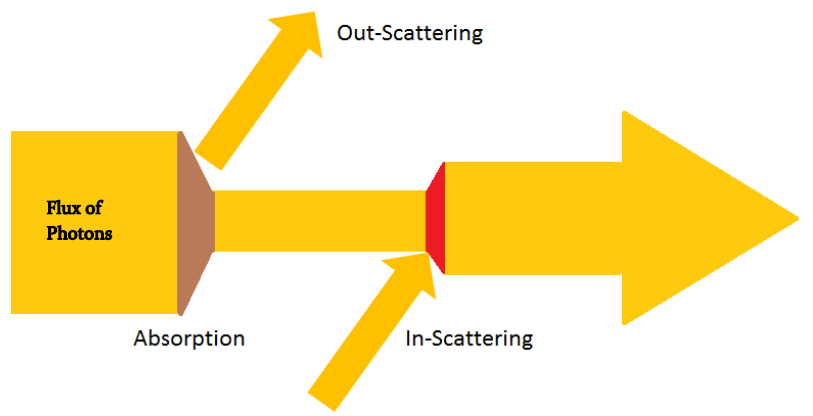
什么是光散射现象?光源的辐射度沿着路径前行时,碰到参与介质时会发生三个不同散射现象的行为:
- 吸收(Absobption): 参与介质把光能量转换为其他形式的能量。
- 外散射(Out-Scattering): 改变光传播方向。
- 内散射(In-Scattering):进入相机方向的入射辐射度。
大气物理模型
如何推导出大气现象背后的物理模型,首先假设大气层只存在一次单散射现象,即视线路径上只发生一次散射。
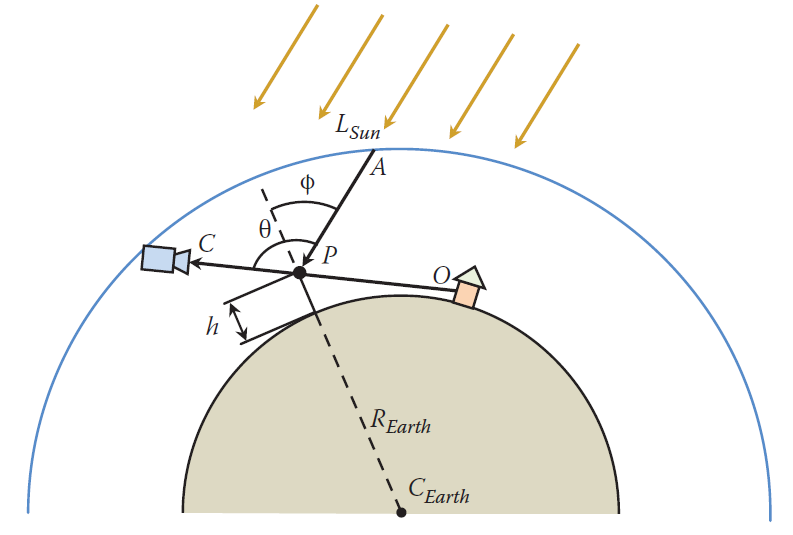
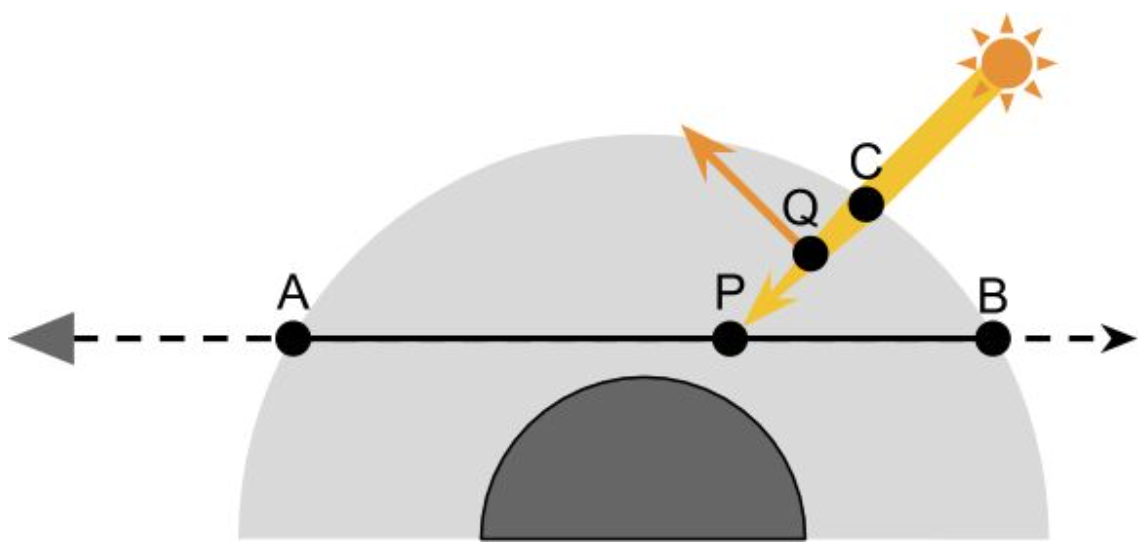
如图,太阳光到达大气层并没有能量损失,在$C$点的光通量为$I_{s}$。由于单散射,路径$CP$上不会发生散射,但是会有光照强度损失,P点的光强为$I_{p} = I_{s}T(\overline{CP})$。在P点的光强只有一部分能量才会转向相机,那么P点散射函数与哪些因素有关呢?
* 角度:相机方向与太阳太阳的夹角。
* 高度:高度不同,粒子的密度值不同。
* 波长:波长较小的光分量更容易被散射。
散射函数细化,可由后面文章的函数组合来表示P点的散射现象。
散射系数
散射系数与粒子的大小,折射率有关。根据粒子大小不同可分为瑞利散射系数和米散射系数。
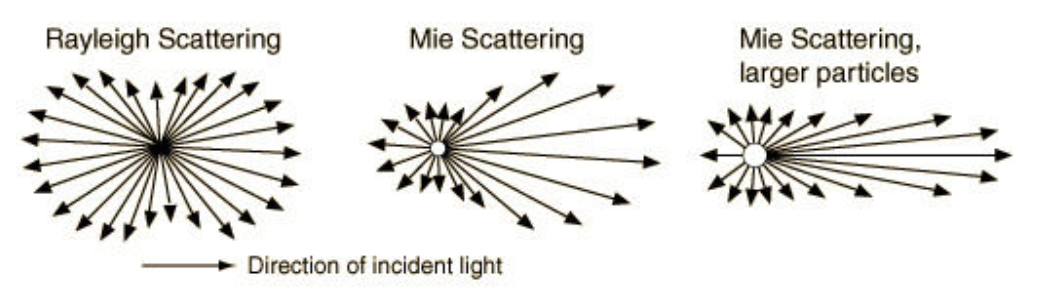
瑞利散射系数?
因为小分子的大小远小于光线波长,这造成了光的波长会影响瑞利散射效果,因此瑞利散射是波长相关。上图左边瑞利散射几乎均匀向四面八方散射光强,这也是白天时候瑞利散射把波长较小的蓝色光向天空四面八方散射造成蓝天效果。
$ \beta_{R}(\lambda) = 8\pi^3\frac{(n^2-1)^2}{3N_{e}\lambda^4} $
其中,$n$是空气的折射率,约等于(1.0003);$N_{e}$是海平面的空气密度,约为2.545e25;$\lambda$是入射光的波长.经过计算,瑞利散射系数可表示为$\beta_{R}^{s}.rgb = (5.8,13.5,33.1)10^{-6}m^{-1}$。
米散射系数?
米散射系数很难去推导计算,基于统计数据的结果,米散射系数可以常量进行估计。[BN08]论文中,米散射系数值为$\beta_{M}^{s} = (2,2,2)10^{-6}m^{-1}$。
相位函数
相位函数表示太阳光发生散射现象时转向相机方向的概率函数。
瑞利相位函数
$F_{R}(\theta) = \frac{3}{4}(1+cos\theta) $米相位函数
米散射相位函数更加复杂,分布变化与粒子大小有关。[CS92]改善了Henyey-Greenstein函数,用来近似计算米散射相位函数。
$F_{M}(\theta, g) = \frac{3(1-g^2)}{2(2+g^2)}\frac{1+\cos^2(\theta)}{(1+g^2-2g\cos^2(\theta))^{3/2}}$
密度函数
根据散射系数和相位函数,我们可以计算海平面的散射值。但是随着海拔高度的增加,空气中的粒子密度是发生变换的,而密度函数是用来估计任意高度下粒子的密度。
$p_{R,M}(h) = exp(-\frac{h}{H_{R,M}})$
其中,h是以海平面为基准的额高度,其中瑞利和米散射海平面基准高度为$H_{R}$8000米,$H_{M}$为1200米。
太阳光通过大气层最终进入视野的只有内散射的光通量,而根据参与介质的类型不同可分为两种散射现象。水分子相关的散射为瑞利散射,气溶胶相关的为米散射。
透射比函数
现在只能确定太阳光转向相机方向的光通量,除了方向还需要计算光强的衰减。计算透射函数之前先了解光学深度的概念。
光学深度
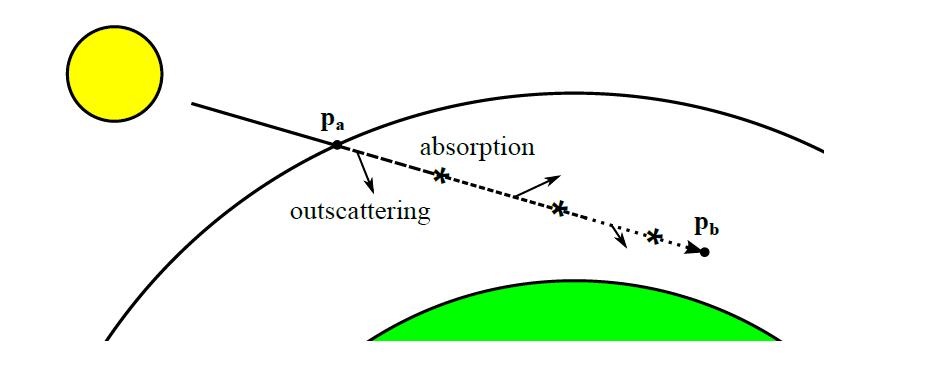
光学深度本质是积分函数,可理解为光强经过长度路径AB后,被空气分子或粒子吸收和外散射后,损失的光通量部分。
$D(A->B) = \int_{A}^{B} (\beta_{R}^{e}e^{-h(t)/H_{R}} + \beta_{M}^{e}e^{-h(t)/H_{M}})dt $
其中,瑞利散射和米散射的光学深度是相互独立且可分别计算,其中散射系数$\beta_{R/M}^{s}$是海平面的数值,还需要被密度函数$e^{-h/H_{R/M}}$进行缩放。光学深度根据公式来看,就是瑞利散射和米散射消光系数和密度函数乘积的积分。
- 瑞利散射消光系数: $\beta_{R}^{e} = \beta_{R}^{s}$,消光系数等于散射系数。
- 米散射消光系数: $\beta_{M}^{e} = \beta_{M}^{s} + \beta_{M}^{a}$,[BN08]论文中建议米散射吸收系数等于散射系数的0.1倍。
透射函数的衰减非线性衰减,也是指数衰减形式,并与光学深度紧密联系。
$T(A->B) = exp^{-D} $
散射积分
上面部分都只考虑了相机方向P点的散射,但是视线方向AB上有无数的P点,通过积分拟合把视线路径AB拆分为无数的线段距离,就可以计算出整个路径上的内散射积分和。
$L_{In} = \int_{C}^{O}L_{Sun}e^{-T(A(s)->P(s))}e^{-T(P(s)->C)} * V(P(s))(\beta_{R}^{s}e^{-h(s)/H_{R}}p_{R}(\theta)+\beta_{M}^{s}e^{-h(s)/H_{M}}p_{M}(\theta)) ds$
大气透视
当看远处的山时,发现会有一种雾蒙蒙的感觉,这是由于远山在视线的路径上发生了透射衰减,此现象也被称为大气透视。以图中O点举例,即O点入射辐射度为自身对象辐射度的衰减和内散射光的积分之和,计算公式为:
$L = L_{O}e^{-T(O->C)} + L_{In}$
大气雾的计算由此而来。

